2022. 10. 2. 18:41ㆍ컴퓨터 구조
[Lecture03] ISA part1.pdf 참고
http://egloos.zum.com/psyoblade/v/2411691
제2장 명령어 - 용어정리 및 요약
1. 명령어 집합(instruction set)특정한 구조가 이해할 수 있는 명령어들의 집합 - 컴퓨터 하드웨어에게 일을 시킬 수 있는 도구, 언어의 집합2. 내장 프로그램(stored-program)개념여러 종류의 데이터와
egloos.zum.com
https://plan0a-0z-entering-security.tistory.com/39
Chapter 2 : Instructions : Language of the Computer
MIPS ISA
Key underlying design principles
- 1. Simplicity favors regularity
- 2. Smaller is faster
- 3. Make the common case fast
명령어 집합 설계자를 위한 설계원칙
1. 간단하기 위해서는 규칙적인 것이 좋다.
: 모든 명령어의 길이를 똑 같게 한 것.
: 산술 명령어는 항상 레지스터 피연산자가 세개로 한 것.
: 어떤 명령어 형식에서나 레지스터 필드의 위치를 일정하게 만든것.
2. 작은 것이 빠르다.
: 레지스터 개수를 32개로 제한한 것.
3. 자주 생기는 일을 빠르게 하라.
: 조건부 분기에 PC-상대 주소를 사용한 것.
: 수치 주소로 상수 피연산자를 사용할 수 있게 만든 것.
😱1. Simplicity favors regularity
all MIPS arithmetic instructions include a single operation & three operands.
(하나의 연산 & 세 개의 피연산자로 구성)
- Regularity makes implementation simpler
- Simplicity enables higher performance at lower cost

ISA = 컴퓨터 언어이자 SW 와 HW간의 interface
예를 들어 보자.
a=b+c+d;라는 C 코드가 있을 때 이것을 컴파일하게 되면 MIPS 코드로 번역하게 되면 아래와 같다.
add a, b, c
add a, a, d
f=(g+h) - (i+j);라는 C 코드가 있다면 이것을 MIPS 코드로 컴파일하게 되면
add t0, g, h
add t1, i, j
sub f, t0, t1
이 된다.

그러나 위 연산들이 실제 MIPS연산은 아니다. 실제 MIPS에서는 변수를 사용하지 않는다.
😱 2. smaller is faster
Operands of MIPS arithmetic instructions must be chosen in a small number of registers.
Register Operands
산술 연산은 register 연산을 사용한다. 레지스터는 매우 빠르고 작은 메모리 공간이다.
레지스터는 processor 내에 특별한 위치에 direct하게 위치하고 있다.
✍️레지스터 : 자주 사용하는 연산 등을 위해 기억해 두는 고속의 전용 영역
MIPS는 32개의 32bit register를 가지고 있다.
자주 사용되고 자주 접근하는 데이터들을 사용하며, 0~31까지 넘버링되어 있다.
✍️word : 하나의 레지스터 데이터

앞에서 봤던 f=(g+h) - (i+j);라는 C 코드를 레지스터를 통한 연산으로 바꾸면 아래와 같은 코드가 된다.



참고) 1 word=4byte=32bit이다.
변수의 자료형 마다 크기가 다르고 byte수도 다르다.
오늘날 int자료형은 대부분 4byte이지만 항상 4byte인 것은 아니다. (컴퓨터의 bit에 따라 다를 수 있다.)
대부분의 정수가 4byte 내에서 표현이 가능하므로 메모리 절약을 위해 4byte를 사용하는 것이다.
만약 64bit 컴퓨터를 사용한다면 int는 8byte가 된다.(컴파일러에서 설정 가능)
32bit 컴퓨터와 64bit 컴퓨터의 차이?
메모리 주소를 위해 사용된 비트의 크기가 다르다. 즉 포인터의 크기를 말한다.
만약 호텔에 여러 개의 방이 존재하고, 그 방의 이름을 오직 두 자리의 정수로만 표현한다면 우리는 00~99까지의 호텔방을 표현할 수 있다.
메모리도 위와 같은 개념이다. 만약 32비트 컴퓨터라면 32비트의 메모리 주소를 갖고 0부터 2^32-1까지의 메모리를 표현할 수 있다. 2^32바이트는 4 * 1024 * 1024 * 1024 이므로 총 4GB 크기의 메모리를 표현할 수 있는 것이다.
따라서 만약 32비트 컴퓨터를 사용한다면 램을 아무리 많이 끼우더라도 실제로 사용 가능한 것은 4GB 메모리까지만 사용이 가능하다. 마찬가지로 64비트 컴퓨터를 사용한다면 총 2^64 크기의 메모리를 사용할 수 있다.
32비트 컴퓨터에는 64비트 OS가 설치가 불가능하다.
하지만 64비트 컴퓨터에는 32비트 OS 설치가 가능하다. 그러나 64비트 컴퓨터에 32비트 OS를 설치한다면 4GB 이상의 메모리는 사용이 불가능하다.
Memory instructions: memory organization
모든 데이터가 레지스터에 저장될 수 없다. 레지스터에는 오직 32개의 공간만 저장이 가능하다.
메인 메모리에는 배열, 자료구조, 동적 데이터(malloc, free)등이 저장된다.
산술 연산을 위해서는 data transfer instruction이 필요하다.
data transfer instruction에는 Load연산과 Store연산이 있다. Load연산은 메모리에 있는 value를 register로 전송하는 것이며 Store연산은 레지스터로부터 결과를 메모리에 저장하는 연산이다.
메모리에 접근하기 위해서는 메모리 주소가 필요하다. 메모리 주소는 위에 설명했듯이 32비트 컴퓨터라면 2^32의 주소에 접근할 수 있고 64비트 컴퓨터라면 2^64 주소에 접근할 수 있다. 메모리 주소는 대게 1 word로 이루어진다.

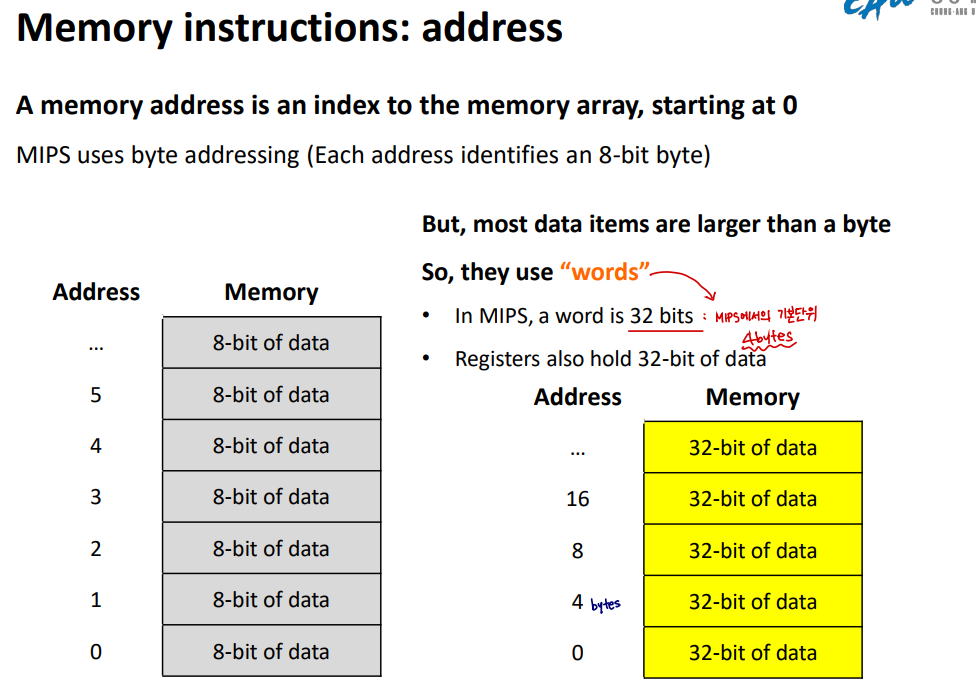
😱 Alignment restrictions
정렬제약 : 메모리 내에서 데이터가 자연스러운 경계를 지켜야한다는 요구조건
ex. 각 데이터의 시작주소는 N의 배수여야 한다. (N : 데이터 사이즈)
- 논리적으로 단순함
- MIPS에서는, words의 시작주소는 4의 배수이다.

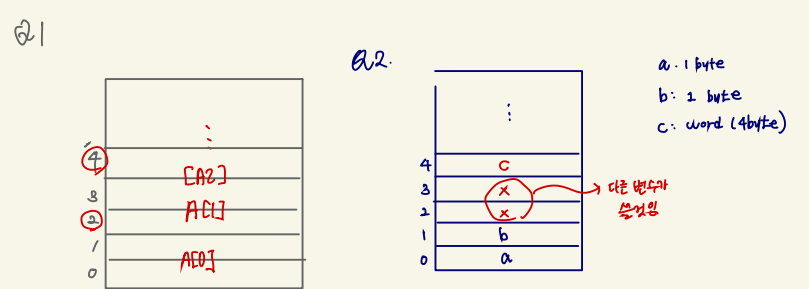
감자의 답 : Q1. 10, Q2. 4
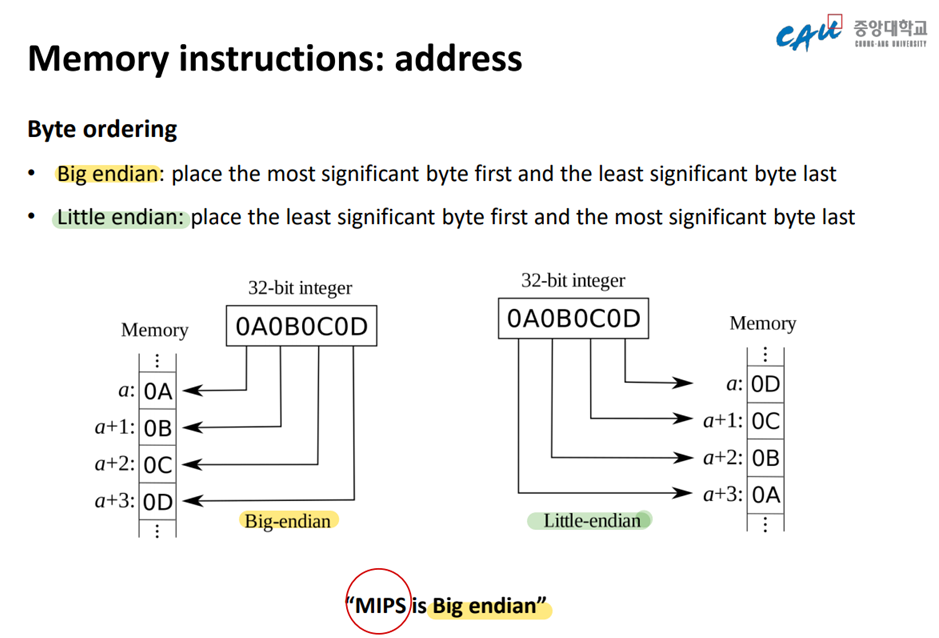
😱 Byte Ordering
Multi-byte 데이터를 저장하는 방법
1. Big Endian
2. Little Endian
예를 들어 10이라는 int형 데이터를 메모리에 저장하려고 한다.
0000 0000 0000 0000 0000 0000 0000 1010
MSB LSB
으로 저장될 것이다. 이 표현은 인간이 읽을 수 있는 방법이다.
MSB(Most-Significant Byte) : 첫 8비트
LSB(Least-Significant Byte) : 맨 뒤 8비트
컴퓨터는 메모리를 1Byte씩 읽어들인다.
Big Endian : MSB가 주소의 lower한 위치에 옴
0000 0000 0000 0000 0000 0000 0000 1010 -> Big Endian 방식
Little Endian : LSB가 주소의 lower한 위치에 옴
1010 0000 0000 0000 0000 0000 0000 0000 -> Little Endian 방식
MIPS는 Big Endian 방식!
😱 Memory Instructions Examples (in MIPS)
lw : load word ( memory -> register )
sw: store word ( register -> memory )
lh : load halfwords
sh : store halfwords
lb : load single byte(8bit) of data
sb : store a single byte(8bit) of data
메모리 연산은 '목적 레지스터, 주소, 베이스 어드레스' 3개의 연산자로 표현된다.
ex.
lw $t0, 32($s3) // $s3레지스터의 32번째 주소에 있는 데이터를 $t0에 load하라
g = h + A [8]; 이라는C 코드를 MIPS코드로 컴파일하면? (A배열은 int형)
g: $s1
h: $s2
A : $s3
lw $t0 32($s3) //A[8]:$t0
add $s1 $s2 $t0

g: $s1
h: $s2
A : $s3
A [12] = h + A [8] 이라는 C 코드를 MIPS코드로 컴파일하게 되면
lw $t0 32($s3) // $t0:A[8]
add $t0 $s2 $t0
sw $t0 48($s3) // 48 : A[12]의 주소

😱 Registers vs. memory
레지스터는 메모리보다 속도가 훨씬 빠르며 사용하기에 간단하다.
메모리에서 계산하면 명령어가 추가적으로 필요함(load, store 등)
memory access에 시간이 너무 오래걸림.
따라서 산술연산은 대부분 레지스터를 사용한다.
컴파일러는 성능향상을 위해 자주 사용하는 작업들을 레지스터로 처리할 필요가 있다.
레지스터 최적화는 프로그램 효율에 큰 영향을 끼친다.
😱 Design principle 3. make the common case fast
작은 상수는 자주 사용한다. 자주 사용되는 작업은 빠르게 해야 한다.
immediate operand(addi)는 load 연산을 생략할 수 있게 해준다.
✍️ addi : add immediate instruction
상수연산을 위해 추가적으로 사용하는 명령어.
immediate operands라고 함
immediate operands를 이용하면 상수(constants)를 로딩하기 위해 메모리에 접근하지 않아도 된다.
add와 addi 다름. addi의 i는 즉시값(immediate)을 가리키며, 형식은 다음과 같다.
addi (rs) (rt) (imm) ; imm은 상수값
add는 operand가 레지스터이지만, addi는 상수값이 존재함.
addi rt, rs, imm #addi (destination), (source), (source) ; 덧셈
addi의 i는 상수값을 의미함.
addi $s0, $s1, 5 // s1레지스터와 5를 더해, s0에 저장한다.
addi $t0, $s3, -12 // s3레지스터와 -12를 더해, t0에 저장



array of bytes : 1바이트 단위의 값을 연속적으로 저장한 배열

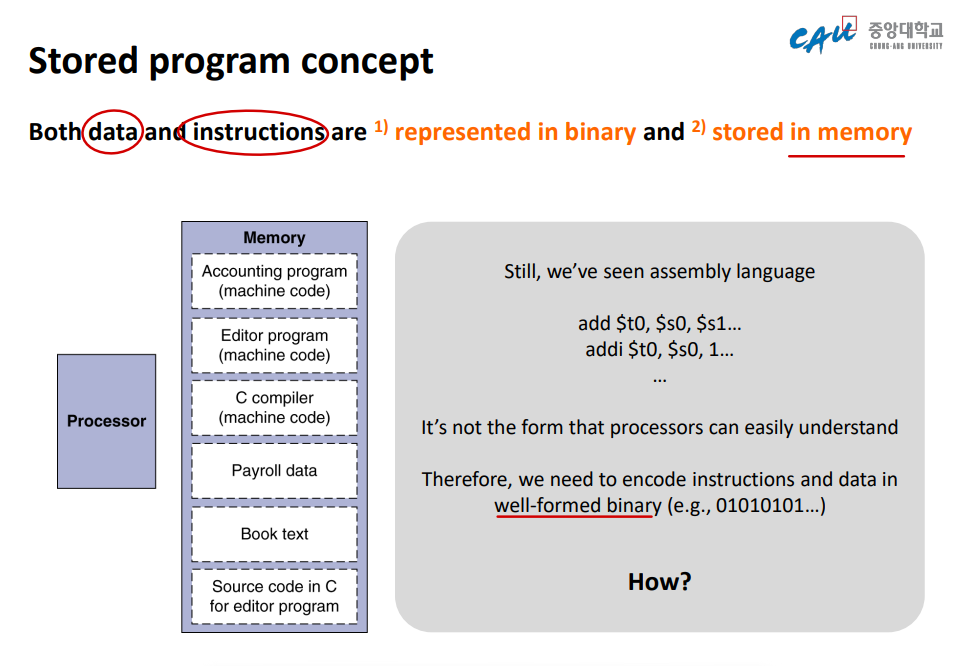
😱 Stored program concept
데이터와 명령어는 모두
1) 2진수로 표현되며
2) 메모리에 저장된다.

😱 Unsigned Binary Integers
비트에 따른 Unsigned Integer의 범위는 어떻게 될까?
음수 값은 고려하지 않으므로 0~2^n-1(n은 bit 수)가 될 것이다.
8bit이라면 0~255가 될 것이며
16bit이라면 0~65535
32bit은 0~4,294,967,295가 된다.
만약 정수 값이 해당 bit를 초과하는 값이라면 overflow가 발생하게 된다.
예를 들어 unsigned 8bit int형 uint8_t a=255에서 a=a+1을 하게 되면 8bit에서 256을 표현하는게 불가능하므로 256이 아닌 0이 저장하게 된다.
😱컴퓨터에서 음수는 어떻게 표현할 수 있을까?
위에서 양수를 표현하는 방식에 대해서는 알아봤다. 음수를 표현하는 방법에는 3가지 방법이 있었다.
첫 번째, Sign & magnitude
이 방식은 첫 비트를(1bit) sign bit로 지정하여 음수를 표현하는 방법이다. sign bit이 1이면 음수를 나타내며 0이면 양수를 나타낸다. sign bit를 제외한 나머지 n-1 bit에서 데이터를 표현해야 하므로 unsigned에 비해 표현 범위는 줄어들게 된다.
그러나 이 방식은 대부분 컴퓨터가 사용하지 않는다. 왜일까?
첫째 이유로는 위 방식으로 '1000 0000'을 표현하면 -0이 된다. '0000 0000' 은 +0이 된다. 즉 똑같은 의미를 가지는 수를 중복하여 표현하고 있다.
둘째 이유로는 만약 -5(1000 0101)과 +5(0000 0101)를 더하게 되면 '10001010'이 되어 -10이라는 엉뚱한 값이 나오게 된다. 따라서 이러한 이유로 많은 컴퓨터 들은 이 방식을 사용하지 않는다.
두 번째, 1`s complement
이 방식은 음수화를 하기 위해 모든 비트를 뒤집는 방식이다.
그러나 이 방식 역시 '0000 0000' 은 +0을 '1111 1111'은 -0을 표현하여 중복된 값을 표현하고 있다.
또한 -5(0000 0101)와 +5(1111 1010)을 더하게 되면 -0이라는 값이 나오게 된다.
이러한 이유로 사람들은 이 방식도 사용하지 않는다.
셋째, 2`s complement
위의 문제들을 해결하기 위하여 사용하는 방식이다.
음수화를 하기 위해 위의 1`s complement에서 했던 것처럼 모든 비트를 뒤집고 1을 더한다.
이렇게 하면 -5(1111 1011)와 +5(00000101)을 더하게 되면 올바른 0000 0000 이 되어 0이 나오게 되고,
+0(0000 0000)을 음수화 하여도 (0000 0000)이 되어 중복된 값을 표현하지 않게 된다.
위의 음수를 표현하는 방식을 이용하여 Signed Integer를 나타낼 수 있다.
첫 번째 bit는 부호를 나타내며 1일 경우 음수를 0일 경우 양수이다.
표현 범위는 '-2^(n-1) ~ 2^(n-1) -1'이다.
8bit이라면 -128 ~ 127
16bit이라면 -32768 ~ 32767
32bit이라면 -2,147,483,648 ~ 2,147,483,647이 된다.
0을 나타내기 위해서는 All zero가 돼야 하며
-1을 나타내기 위해서는 All one이 되어야 한다.
또한, 가장 큰 음수 값은 1000 0000... 0000이며
가장 큰 양수 값은 0111 1111... 1111 이 된다.
음수화를 하는 방법을 간단하게 표현하면 "모든 비트를 뒤집고 1을 더하라"로 요약할 수 있다.
만약 8bit에 저장되어 있는 값을 16bit에 옮기면 어떻게 될까?
char a=-5;
int b=a;
라는 코드를 실행시켜보면 b에는 정상적으로 -5라는 값이 들어가게 된다.
이것이 가능한 이유는 sign bit를 왼쪽 모든 비트에 복사하기 때문이다.
예를 들어 8bit에서 2(0000 0010)가 있을 때 이를 16bit으로 옮기게 되면 (0000 0000 0000 0010)이 된다.
-2(1111 1110)를 16bit으로 옮기면 (1111 1111 1111 1110)이 된다.

이러한 bit들을 일일이 적고 읽는 것은 굉장히 힘든 작업이다. 이를 해결하기 위해 4bit마다 비트를 compact 하여 나타낼 수 있다 이를 16진법(Hexadecimal)이라고 한다.
예를 들어 1110 1100 1010 1000 0110 0100 0010 0000을 16진법으로 나타내게 되면
e(1110) c(1100) a(1010) 8(1000) 6(0110) 4(0100) 2(0010) 0(0000) 즉, eca86420(hex)로 나타낼 수 있다.
메모리에 저장되는것은 결국 비트값일 뿐이다.
중요한 것은 우리가 그 비트들을 어떻게 해석하냐에 달려있다.
만약 int a=-5;라는 코드를 통해 메모리에 -5를 저장하려고 한다. 어떻게 저장될까 ?
1111 1111 1111 1111 1111 1111 1111 1011이 될것이다. 만약 Little endian방식의 컴퓨터 라면
1111 1011 1111 1111 1111 1111 1111 1111 로 메모리에 저장이 될 것이다.
우리가 만약 a라는 값을 %d(signed print)로 확인해본다면 -5라는 값이 정상적으로 출력될 것이다.
그런데, a라는 값을 %u(unsigned print)로 확인한다면 어떤값이 나올까? 5가 나올까?
4294967291라는 전혀 엉뚱한 값이 나오게된다. 어떻게 이 값이 나오게 된것일까?
메모리에는 위에 적은대로 1111 1011 1111 1111 1111 1111 1111 1111 라는 비트가 저장되어 있다.
그러나 이 메모리를 우리가 어떻게 읽어들이냐에 따라 값은 다르게 나올것이다.
%d로 읽는다면 부호를 고려해야 하므로 첫번째 bit를 사인비트로 사용하여 -5라는 값을 정상적으로 출력할 것이다.
그러나 %u로 읽는다면 우리는 사인비트를 고려하지 않는다. 따라서 1111 1011 1111 1111 1111 1111 1111 1111라는값을 그대로 읽어 4294967291이라는 값이 나오게 되는것이다.


😱 Instruction representation
데이터와 마찬가지로, 명령어도 2진수로 encoding되고 표현된다.
인코드 (encode): 주어진 정보를 어떤 프로그램에 대응하는 형태로 부호화하여 입력하는 일.
machine instructions = encoded instructions
인코딩되지 않은 명령여 예시 => assembly language //ex. add $t0, $t1, $t2
명령어를 표현하기 위해 ISA는 instruction formats(layout of instructions)을 정의한다.
예를 들어 인코딩된 비트 나열에서 어떤 부분을 어떻게 사용할지 등
문제는 모든 종류의 instructions을 표현하기 위해서는 많은 instruction format을 사용해야 한다는 것이다.
다른 format을 디코딩하려면 컴퓨터 구조도 복잡해져야 한다.
😱 Design principle 4. Good design demands good compromise
#설계원칙4_ 좋은 설계는 좋은 절충안을 요구함

'컴퓨터 구조' 카테고리의 다른 글
| 컴퓨터 구 lecture note #06 (0) | 2022.10.09 |
|---|---|
| 컴퓨터 구조 lecture note #05 (0) | 2022.10.06 |
| 컴구 lecture note #03 (0) | 2022.09.18 |
| 컴구 lecture note #02 (2) | 2022.09.08 |