👩‍💻중앙대 자료구조 assignment#3_Find MST using Kruskal alg.(C언어, C++)

👻kruskal 알고리즘은 대회에서 자주 출제된다!

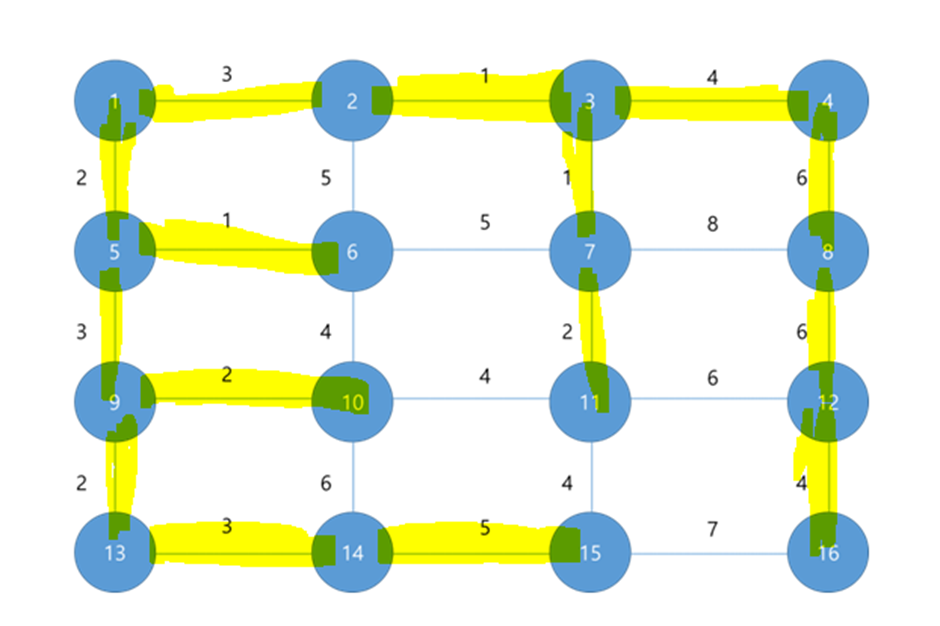
1. Implements the following graph as an adjacency list.

 

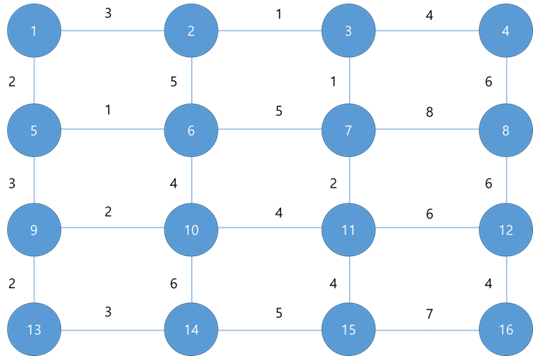
2. Find the minimum spanning tree (MST) using the Kruskal method.

 

3. Find the shortest path from vertex # 1 in the graph to all vertices.

--------------------------------------------------------------------------------------------------------------------------------------------------------

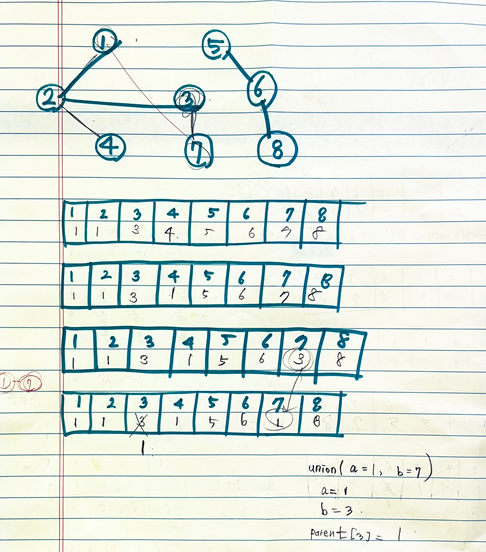
👻노드가 같은 그래프에 속해있는지 확인하기 위해 union- find(합집합 찾기) 알고리즘을 먼저 알아야 한다.

https://www.youtube.com/watch?v=AMByrd53PHM 

https://m.blog.naver.com/ndb796/221230967614

17. Union-Find(합집합 찾기)

#include <stdio.h>
//Union_Find
int getParent(int parent[], int x) {
	if (parent[x] == x)
		return x;
	return parent[x] = getParent(parent, parent[x]);
}

//각 부모 노드를 합칩니다.
void unionParent(int parent[], int a, int b) {
	a = getParent(parent, a);
	b = getParent(parent, b);
	if (a < b)
		parent[b] = a;
	else {
		parent[a] = b;
	}
}

//같은 부모 노드를 가지는지 확인합니다.
//같은 그래프에 속해있는지 확인하는 것과 동일
int findParent(int parent[], int a, int b) {
	a = getParent(parent, a);
	b = getParent(parent, b);
	if (a == b)return 1;
	else return 0;
}

int main(void) {
	int parent[9];
	for (int i = 1; i <= 8; i++) {
		parent[i] = i;
	}

	unionParent(parent, 1, 2);
	unionParent(parent, 2, 3);
	unionParent(parent, 5, 6);
	unionParent(parent, 6, 8);
	unionParent(parent, 1, 8);

	printf("1과 3는 연결되어있나요? %d\n", findParent(parent, 1, 3));
	printf("3과 8은 연결되어있나요? %d\n", findParent(parent, 3, 8));

}

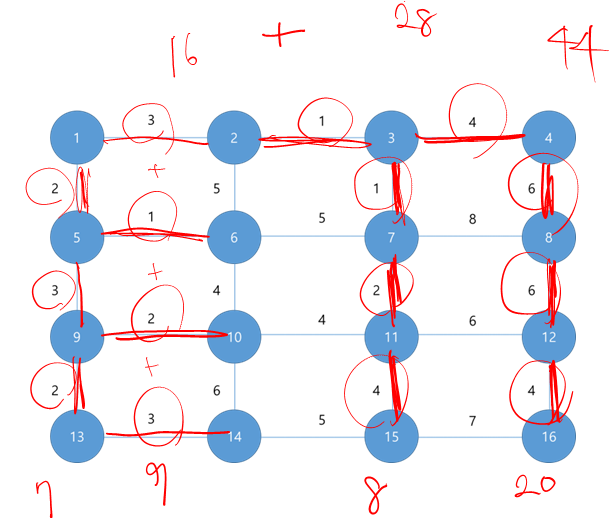
👻비용을 기준으로 오름차순으로 정렬

 

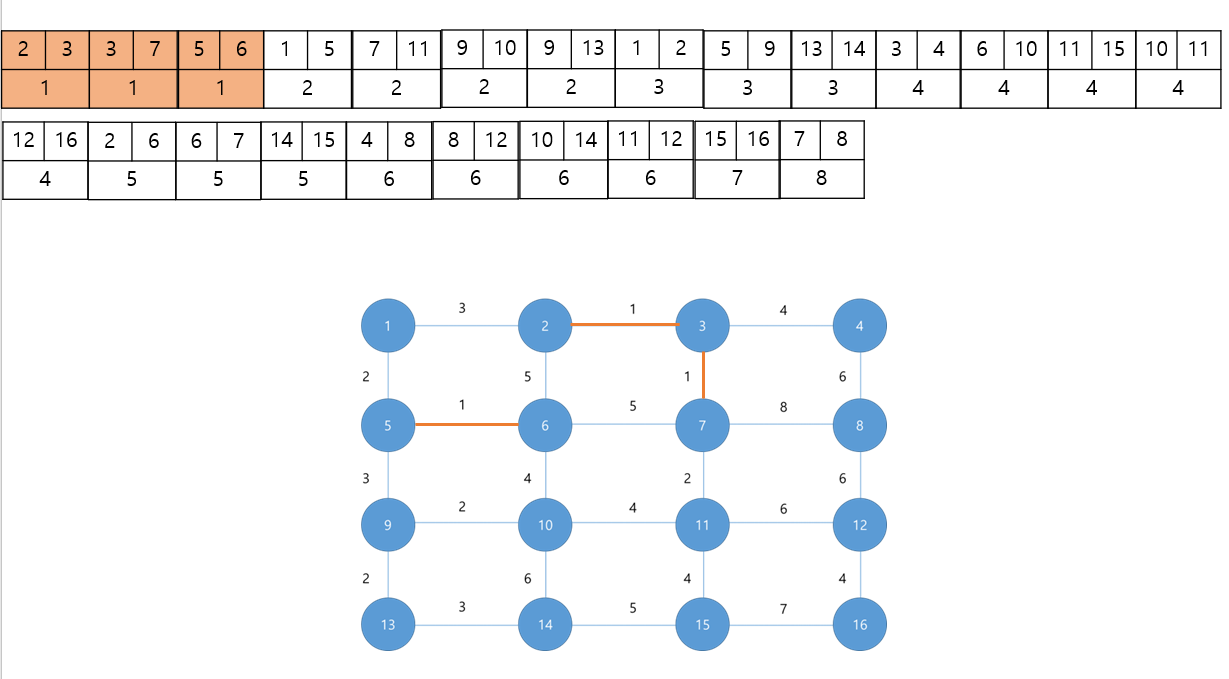
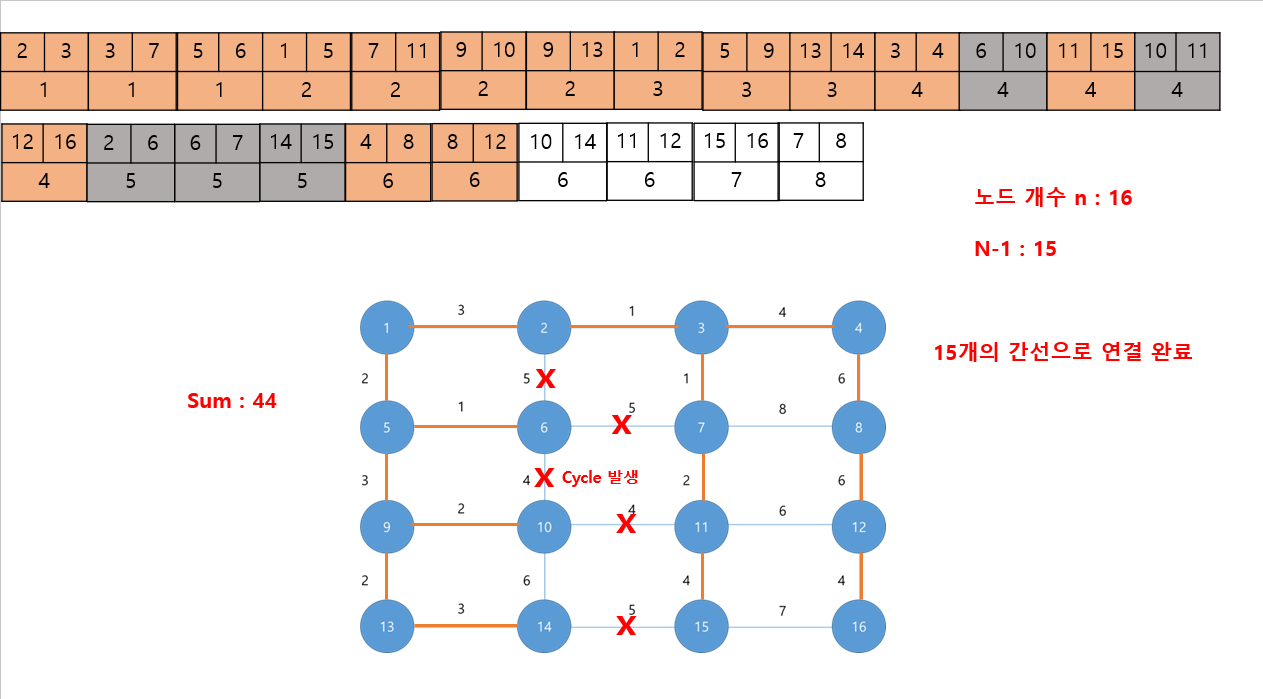
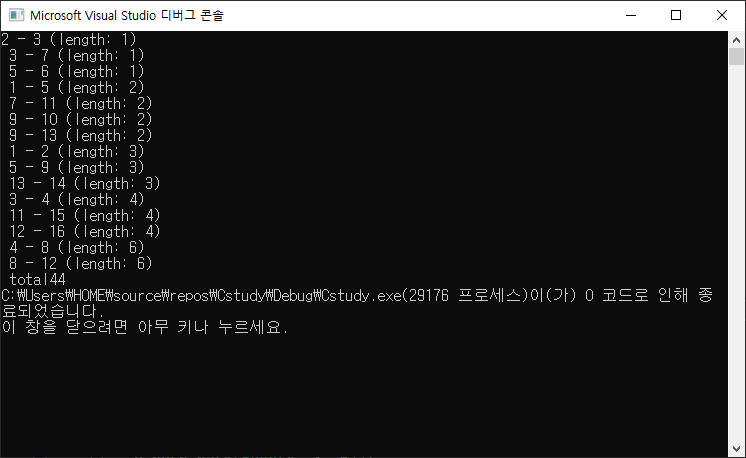
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

//부모 노드를 가져옴
int getParent(int parent[], int x) {
	if (parent[x] == x)
		return x;
	return parent[x] = getParent(parent, parent[x]);
}

//각 부모 노드를 합칩니다.
void unionParent(int parent[], int a, int b) {
	a = getParent(parent, a);
	b = getParent(parent, b);
	if (a < b)
		parent[b] = a;
	else {
		parent[a] = b;
	}
}

//같은 부모 노드를 가지는지 확인합니다.
//같은 그래프에 속해있는지 확인하는 것과 동일
int findParent(int parent[], int a, int b) {
	a = getParent(parent, a);
	b = getParent(parent, b);
	if (a == b)return 1;
	else return 0;
}

//간선 클래스 선언
class Edge {
public:
	int node[2]; //서로 연결된 두개의 노드정보
	int distance;
	Edge(int a, int b, int distance) {
		this->node[0] = a;
		this->node[1] = b;
		this->distance = distance;
	}
	bool operator <(Edge &edge) {
		return this->distance < edge.distance;
		//거리가 작은 순으로 출력
	}
};

int main(void) {
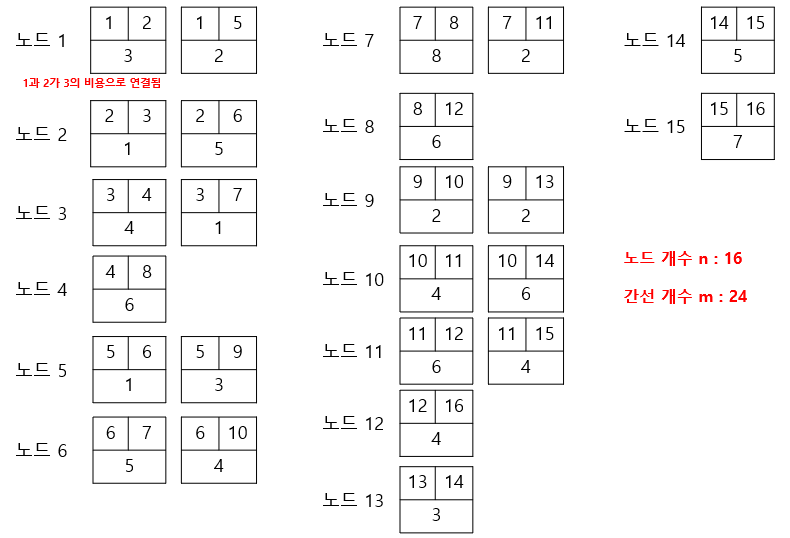
	const int n = 16;//노드개수
	const int m = 24; //간선개수
	//24  79 - 55 = 24
	vector<Edge> v;
	v.push_back(Edge(1, 2, 3)); //1과 2가 비용이 3인 간선으로 연결됨
	v.push_back(Edge(1, 5, 2));
	v.push_back(Edge(2, 6, 5));
	v.push_back(Edge(2, 3, 1));
	v.push_back(Edge(3, 7, 1));
	v.push_back(Edge(3, 4, 4));
	v.push_back(Edge(4, 8, 6));
	v.push_back(Edge(5, 6, 1));
	v.push_back(Edge(5, 9, 3));
	v.push_back(Edge(6, 7, 5));
	v.push_back(Edge(6, 10, 4));
	v.push_back(Edge(7, 8, 8));
	v.push_back(Edge(7, 11, 2));
	v.push_back(Edge(8, 12, 6));
	v.push_back(Edge(9, 10, 2));
	v.push_back(Edge(9, 13, 2));
	v.push_back(Edge(10, 11, 4));
	v.push_back(Edge(10, 14, 6));
	v.push_back(Edge(11, 12, 6));
	v.push_back(Edge(11, 15, 4));
	v.push_back(Edge(12, 16, 4));
	v.push_back(Edge(13, 14, 3));
	v.push_back(Edge(14, 15, 5));
	v.push_back(Edge(15, 16, 7));

	//간선의 비용을 기준으로 오름차순 정렬
	sort(v.begin(), v.end()); //<algorithm>에 포함

	//각 정점이 포함된 그래프가 어디인지 저장
	int parent[n];
	for (int i = 0; i < n; i++) {
		parent[i] = i;
	}

	printf("Find the shortest path from vertex #1 in the graph to all vertices.\n");
	int sum = 0;
	for (int i = 0; i < v.size(); i++) {
		//사이클이 발생하지 않는 경우 그래프에 포함
		if (!findParent(parent, v[i].node[0] - 1, v[i].node[1] - 1)) {
			sum += v[i].distance; //거리총합에 저장
			printf("%d - %d (length: %d)\n ", v[i].node[0], v[i].node[1], v[i].distance);
			unionParent(parent, v[i].node[0] - 1, v[i].node[1] - 1);//두개의 노드 연결
		}
	}

	printf("total%d", sum);
	//return 0; 
}

 

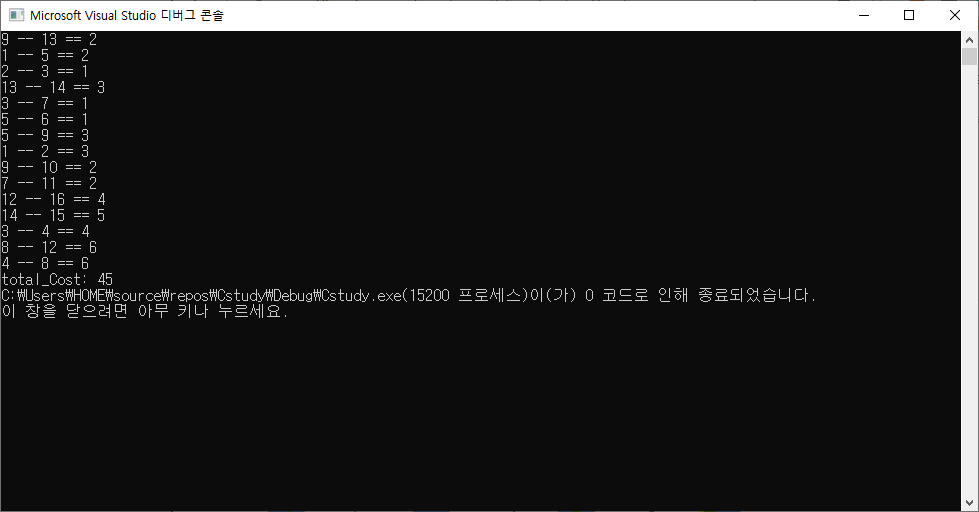
👻망했다. C++라이브러리 사용하지 말라고 하셔서 C로 다시 구현해야된다. 왕귀찮다.

데이터 입력할때는 0부터로 바꿔주고 출력할때 다시 되돌려놓겠다는 뜻

#include <stdio.h>
#include <stdlib.h>

int total_cost;


struct Edge
{
	int Source;
	int Destination;
	int Weight;
};

struct Graph
{
	int VerticesCount;
	int EdgesCount;
	struct Edge* Edge;
};

struct Subset
{
	int Parent;
	int Rank;
};


struct Graph* CreateGraph(int verticesCount, int edgesCoun)
{
	struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
	graph->VerticesCount = verticesCount;
	graph->EdgesCount = edgesCoun;
	graph->Edge = (struct Edge*)malloc(graph->EdgesCount * sizeof(struct Edge));

	return graph;
}

int Find(struct Subset subsets[], int i)
{
	if (subsets[i].Parent != i)
		subsets[i].Parent = Find(subsets, subsets[i].Parent);

	return subsets[i].Parent;
}

void Union(struct Subset subsets[], int x, int y)
{
	int xroot = Find(subsets, x);
	int yroot = Find(subsets, y);

	if (subsets[xroot].Rank < subsets[yroot].Rank)
		subsets[xroot].Parent = yroot;
	else if (subsets[xroot].Rank > subsets[yroot].Rank)
		subsets[yroot].Parent = xroot;
	else
	{
		subsets[yroot].Parent = xroot;
		++subsets[xroot].Rank;
	}
}

int CompareEdges(const void* a, const void* b)
{
	struct Edge* a1 = (struct Edge*)a;
	struct Edge* b1 = (struct Edge*)b;
	return a1->Weight > b1->Weight;
}

void Print(struct Edge* result, int e)
{
	for (int i = 0; i < e; ++i) {
		printf("%d -- %d == %d\n", result[i].Source, result[i].Destination, result[i].Weight);
		total_cost += result[i].Weight;
	}
		

}

void Kruskal(struct Graph* graph)
{
	int verticesCount = graph->VerticesCount;
	struct Edge* result = (struct Edge*)malloc(sizeof(result) * verticesCount);
	int i = 0;
	int e = 0;

	qsort(graph->Edge, graph->EdgesCount, sizeof(graph->Edge[0]), CompareEdges);

	struct Subset* subsets = (struct Subset*) malloc(verticesCount * sizeof(struct Subset));

	for (int v = 0; v < verticesCount; ++v)
	{
		subsets[v].Parent = v;
		subsets[v].Rank = 0;
	}

	while (e < verticesCount - 1)
	{
		struct Edge nextEdge = graph->Edge[i++];
		int x = Find(subsets, nextEdge.Source);
		int y = Find(subsets, nextEdge.Destination);

		if (x != y)
		{
			result[e++] = nextEdge;
			Union(subsets, x, y);
		}
	}

	Print(result, e);
}

void main() {

	int verticesCount = 16;
	int edgesCount = 24;
	struct Graph* graph = CreateGraph(verticesCount, edgesCount);

	// Edge 0-1
	graph->Edge[0].Source = 0;
	graph->Edge[0].Destination = 1;
	graph->Edge[0].Weight = 3;

	// Edge 0-4
	graph->Edge[1].Source = 0;
	graph->Edge[1].Destination = 4;
	graph->Edge[1].Weight = 2;

	// Edge 1-2
	graph->Edge[2].Source = 1;
	graph->Edge[2].Destination = 2;
	graph->Edge[2].Weight = 1;

	// Edge 2-3
	graph->Edge[3].Source = 2;
	graph->Edge[3].Destination = 3;
	graph->Edge[3].Weight = 4;

	// Edge 2-6
	graph->Edge[4].Source = 2;
	graph->Edge[4].Destination = 6;
	graph->Edge[4].Weight = 1;

	
	// Edge 4-5
	graph->Edge[5].Source = 4;
	graph->Edge[5].Destination = 5;
	graph->Edge[5].Weight = 1;

	// Edge 4-8
	graph->Edge[6].Source = 4;
	graph->Edge[6].Destination = 8;
	graph->Edge[6].Weight = 3;

	// Edge 5-6
	graph->Edge[7].Source = 5;
	graph->Edge[7].Destination = 6;
	graph->Edge[7].Weight = 5;

	// Edge 6-7
	graph->Edge[8].Source = 6;
	graph->Edge[8].Destination = 7;
	graph->Edge[8].Weight = 8;

	// Edge 6-10
	graph->Edge[9].Source = 6;
	graph->Edge[9].Destination = 10;
	graph->Edge[9].Weight = 2;

	// Edge 7-11
	graph->Edge[10].Source = 7;
	graph->Edge[10].Destination = 11;
	graph->Edge[10].Weight = 6;

	// Edge 8-9
	graph->Edge[11].Source = 8;
	graph->Edge[11].Destination = 9;
	graph->Edge[11].Weight = 2;

	// Edge 8-12
	graph->Edge[12].Source = 8;
	graph->Edge[12].Destination = 12;
	graph->Edge[12].Weight = 2;

	// Edge 9-10
	graph->Edge[13].Source = 9;
	graph->Edge[13].Destination = 10;
	graph->Edge[13].Weight = 4;

	// Edge 9-13
	graph->Edge[14].Source = 9;
	graph->Edge[14].Destination = 13;
	graph->Edge[14].Weight = 6;

	// Edge 10-11
	graph->Edge[15].Source = 10;
	graph->Edge[15].Destination = 11;
	graph->Edge[15].Weight = 6;

	// Edge 10-14
	graph->Edge[16].Source = 10;
	graph->Edge[16].Destination = 14;
	graph->Edge[16].Weight = 4;

	// Edge 11-15
	graph->Edge[17].Source = 11;
	graph->Edge[17].Destination = 15;
	graph->Edge[17].Weight = 4;

	// Edge 12-13
	graph->Edge[18].Source = 12;
	graph->Edge[18].Destination = 13;
	graph->Edge[18].Weight = 3;

	// Edge 13-14
	graph->Edge[19].Source = 13;
	graph->Edge[19].Destination = 14;
	graph->Edge[19].Weight = 5;

	// Edge 14-15
	graph->Edge[20].Source = 14;
	graph->Edge[20].Destination = 15;
	graph->Edge[20].Weight = 7;

	// Edge 3-7
	graph->Edge[21].Source = 3;
	graph->Edge[21].Destination = 7;
	graph->Edge[21].Weight = 6;

	// Edge 5-9
	graph->Edge[22].Source = 5;
	graph->Edge[22].Destination = 9;
	graph->Edge[22].Weight = 4;

	// Edge 1-5
	graph->Edge[23].Source = 1;
	graph->Edge[23].Destination = 5;
	graph->Edge[23].Weight = 5;

	Kruskal(graph);
	printf("total_Cost: %d", total_cost);
}